Kinda late to the party with those four, but here goes. The supercomputer binary involved 4 challenges, retrieving 4 numbers out of a binary for 50, 50, 100, and 300 points respectively. Didn’t solve them on time, but it’s a good reversing challenge.
Supercomputer 1 [50] Pirating
Computing one big number is hard, but apparently the robots can do four? Please help us!
What is the first number?
main() is at 0x400674. A state vector is initialized, seen below:
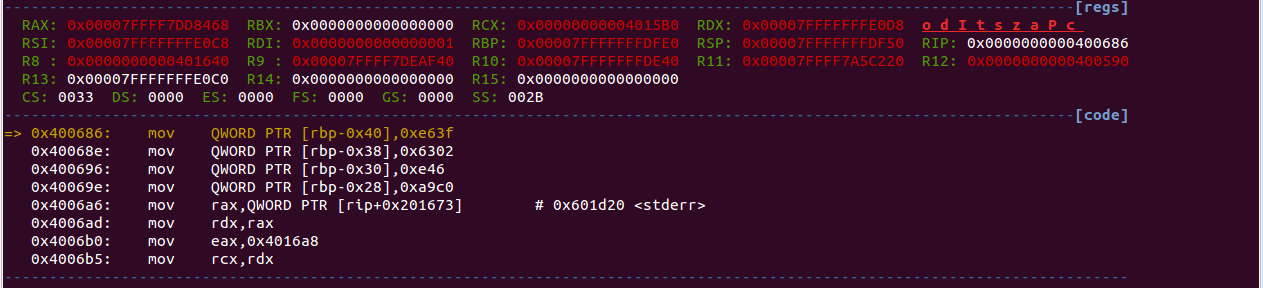
and the fun begins. By running the executable you can see a “progress report” with dots
and first thing we notice are calls to sleep. Did I mention the progress is super slow?
Apparently, you have to speed it up. Being the naive fellow I am, I initially just
LD_PRELOADed them out, but the process kept slowing down, forcing me to be clever. We
nop the calls to sleep, and resort to callgrind, which shows us the (first) culprit:
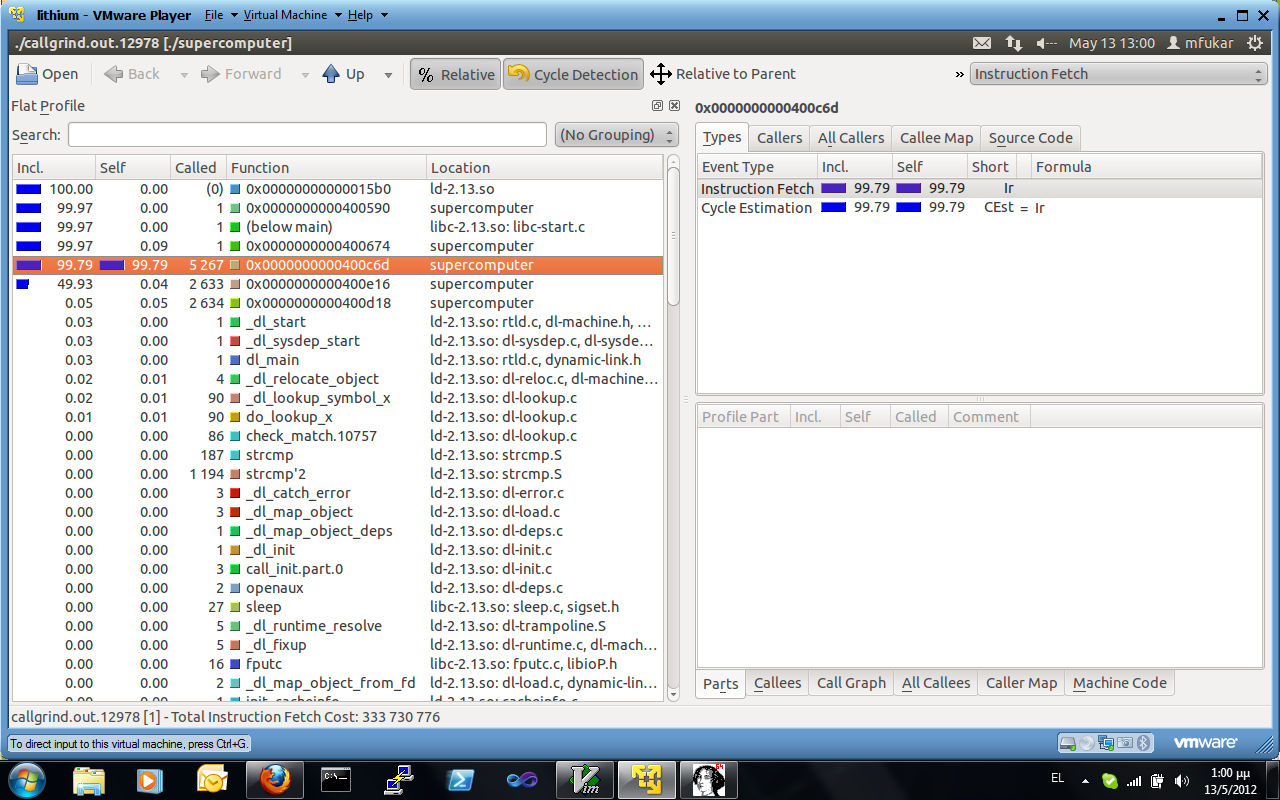
which is a particularly laid back way of performing addition (+1 in a loop). We patch it with the following (NASM syntax everywhere).
(Patches given in assembly have jumps relative to the address given at the start of each snippet)
After the loop has terminated, there is an integrity check of the third state vector entry
(done for all four keys, actually). If it passes, the concatenation of (state[0] +
state[1]) and (state[2] + state[3]) is output as the first key, which is:
Yay! The first key is 414e0d423f5fcd195a579f95f1ff6525
For the key generation, there are multiple functions involved (there are jump tables at
addresses 0x601ce0 and 0x401808). However, we don’t need to mess with all of them - just
the very slow ones. The key update functions are selected with a congruence modulo
relation (look for movabs & imul sequences in the disassembly, there are a handful and
are used for other stuff as well). For the second key, the slow function is at 0x400edc,
and is doing a multiplication by addition. We patch it
as well:
Hooray! The second key is f811f0e8a1f9196e27eef9e23eff6367
Alright. For the third key, the slow function is at 0x4010b8, and it’s tricky. After another slow multiplication, it performs a division by repeatedly adding a negative in two’s complement number (0xfffffffef4143e05). We can do better than that:
Hooray! The third key is c9e6d35ed6007b35f7d01a98f6d548fb
The last part is kind of crazy. After hopelessly trying to deduce what to optimize away in the function at 0x400d18, which callgrind reports as the busiest bee in the hive, I decided to take a step back, to its callers. They are two, in a single function at 0x401330, which is in turn called by 0x4011be (via a jump table). If you notice the locals at runtime, you’ll see these functions operate on temporary key vectors and aren’t used to update the original, as far as I could tell. They do go on for an obscene amount of iterations, though, so let’s just skip them altogether, and after a short while..
Congratz! The last key is f9b02fabc4b866288d7c4c5bbcd5507e
Huzzah.
« Past Future »